When we were in school, we were taught to memorize algorithms, rhymes and math facts. For some people, this worked. But for most- they hated math, thought they weren’t good at math, didn’t understand numbers and/or forgot the rhythms and algorithms. Math education looks so different now is most classrooms. Teachers are showing kids WHY and giving them multiple strategies that focus on place value. Students are being taught to make models, or simple drawings, to show or prove their work. These drawings don’t always come naturally and often require lots of concrete practice with manipulatives. But the times is well spent. Students remember what to do and, more importantly, why they are doing it.
One of the biggest skills taught in the 3rd grade is multiplication. I love teaching it using all kinds of manipulatives and models. Here are five models that I teach my 3rd graders.
This is probably the most basic multiplication model. It really helps to reenforce the concept of multiplication as a collection of equal groups. The first factor in the math fact tells how many groups there are. Students draw a circle for each group. The second factor tells students how many objects are in each group. They can draw Xs inside each of the circles. Now students can count each X, skip count the circles or use repeated addition to solve for the product.
I think that it feels very natural to teach the number bond model after teaching equal groups. Again, it makes it easy to see the repeated addition. This model is easier to draw because the student uses numbers instead of Xs. However, this is a bit more abstract and your intervention group may need more time before jumping to this model. The large circle represents the whole or the product. Each of the smaller circles represents a part or a group. The number inside the small circle represents the number inside each group.
I call this model a tape diagram because of the math curriculum we use. If you are familiar with Singapore Math, they call this a bar model. Either way- it is an amazing model. It typically becomes my students’ favorite because it can be used with any operation and with multi-step problems. It also is a good precursor for fraction models. The entire tape represents the whole or the product. The tape is then divided into equal groups. The number inside represents the size of each group or unit.
This model quickly becomes my students’ favorite model! If you want to read more about it, I HIGHLY recommend the book Step by Step Model Drawing: Solving Word Problems the Singapore Way
. It has tons of samples and ideas for teaching the model for every operation. It’s a game changer!
. It has tons of samples and ideas for teaching the model for every operation. It’s a game changer!
I teach arrays because it really helps students to best understand how and why the multiplication chart works. It will also help lay the foundation for solving for area. An array is also easy to use when demonstrating the distributive property. You can have one large array and use a line to break it in half to make two smaller arrays. The only downside is that the students must draw all the Xs and sometimes they are a bit sloppy with this. Graph paper makes it neater! The first factor tells the students how many groups or rows to draw. The second factor tells how many are in each group. When it is all drawn, students can skip count the rows to solve.
A number line tends to be a bit more abstract than the other models. I like to use it though because I believe it lays the foundation for using a number line for elapsed time. The first number tells the student how many jumps they will make. The second factor tells the student how large each jump will be. They will need to be able to add or skip count to make this model efficient. If they have to draw in every line and count- it takes far too long.
Some final thoughts….
Teaching math models requires lots of modeling from the teacher. I typically use word problems when teaching math modeling rather than just a fact. However, students do want to draw bananas if the problem is about bananas. That is why I always call them models instead of drawings. I remind students that this is not art class!
Not all of my kiddos will master all five of these models. And that is ok! I have given them several tools for their toolbox and they can choose the one that they are most successful with. Most of my kids will master several of these models and will have a strategy to use when checking their work.
I require that my kids use some sort of math model for every math problem. We have a problem solving routine that helps them to be consistent. You can read more about that by clicking on the picture below.
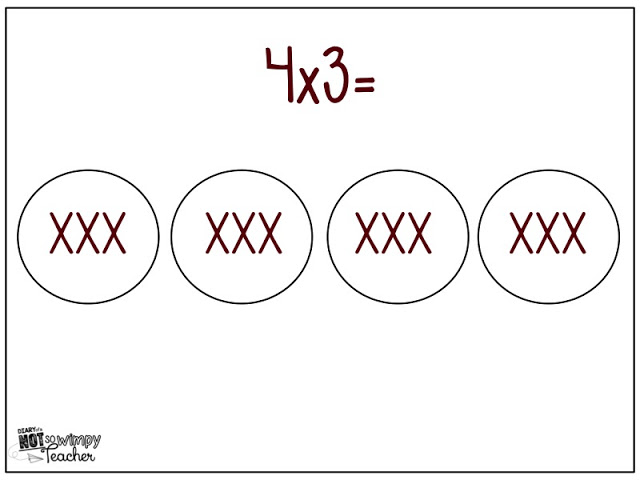
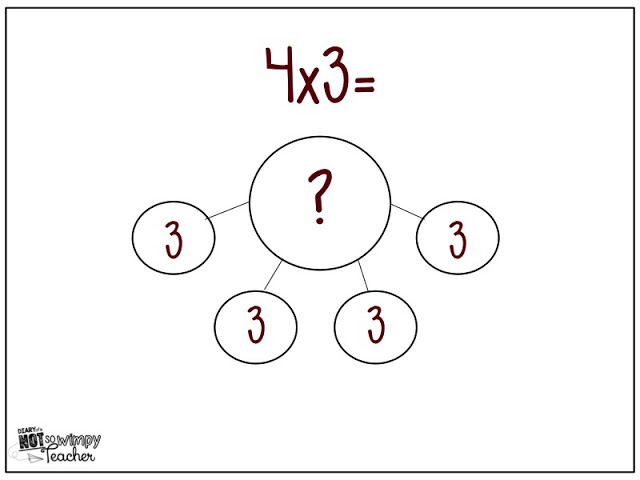
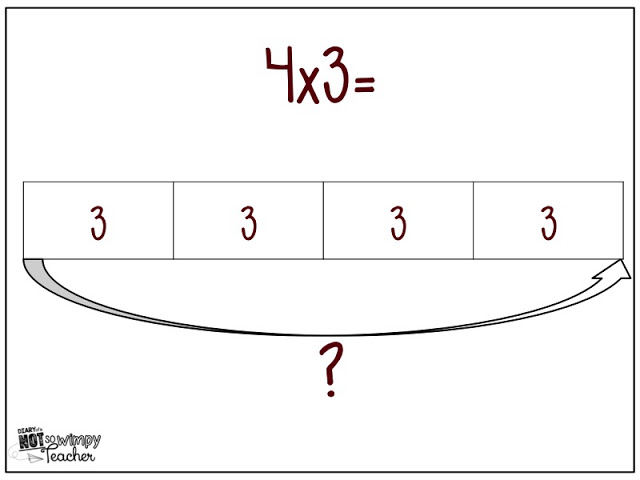
I love the number bond idea! I had never seen that before!!! Thanks for sharing.
I love the number bond idea also! Most of my students should be familiar with that because I know that was used alot in first grade with them. I can''t wait to try this tomorrow!
I was looking for some good blogs related to maths hopefully your article will help to solve my problems in this subject.Thanks for sharing.
You’re welcome! I hope this information is helpful, enjoy!